Automatic Differentiation (AD) is a general and powerful technique for computing partial derivatives (or the complete gradient) of a function inputted as a computer program.
It takes advantage of the fact that any computation can be represented as a composition of simple operations / functions - this is generally represented in a graphical format and referred to as the computation graph. AD works by repeatedly applying the chain rule over this graph.
Efficient computation of gradients is a crucial requirement in the fields of scientific computing and machine learning, where approaches like Gradient Descent are used to iteratively converge over the optimum parameters of a mathematical model.
Within the context of computing, there are various methods for differentiation:
Manual Differentiation: This consists of manually applying the rules of differentiation to a given function. While straightforward, it can be tedious and error-prone, especially for complex functions.
Numerical Differentiation: This method approximates the derivatives using finite differences. It is relatively simple to implement but can suffer from numerical instability and inaccuracy in its results. It doesn’t scale well with the number of inputs in the function.
Symbolic Differentiation: This approach uses symbolic manipulation to compute derivatives analytically. It provides accurate results but can lead to lengthy expressions for large computations. It requires the computer program to be representable in a closed-form mathematical expression, and thus doesn’t work well with control flow scenarios (if conditions and loops) in the program.
Automatic Differentiation (AD): Automatic Differentiation is a general and an efficient technique that works by repeated application of the chain rule over the computation graph of the program. Given its composable nature, it can easily scale for computing gradients over a very large number of inputs.
Automatic Differentiation works by applying the chain rule and merging the derivatives at each node of the computation graph. The direction of this graph traversal and derivative accumulation results in two approaches:
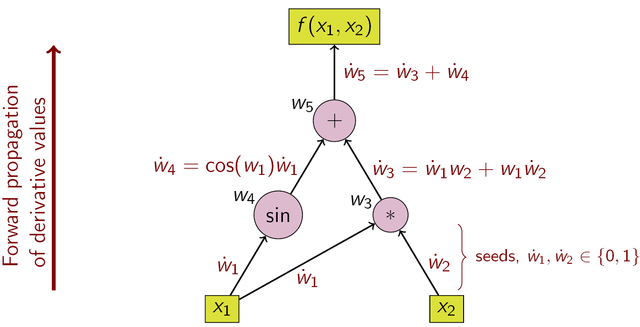
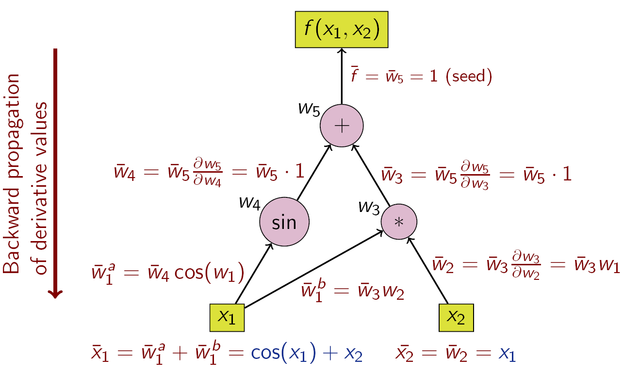
Automated Differentiation implementations are based on two major techniques: Operator Overloading and Source Code Transformation. Compiler Research Group’s focus has been on exploring the Source Code Transformation technique, which involves constructing the computation graph and producing a derivative at compile time.
The source code transformation approach enables optimization by retaining all the complex knowledge of the original source code. The compute graph is constructed during compilation and then transformed to generate the derivative code. The drawback of that approach in many implementations is that, it typically uses a custom parser to build code representation and produce the transformed code. It is difficult to implement (especially in C++), but it is very efficient, since many computations and optimizations can be done ahead of time.
Automatic Differentiation can calculate derivatives without any additional precision loss.
It is not confined to closed-form expressions.
It can take derivatives of algorithms involving conditionals, loops, and recursion.
It can be easily scaled for functions with a very large number of inputs.
Implementing Automatic Differentiation from the ground up can be challenging. However, several C++ libraries and tools are available to simplify the process. The Compiler Research Group has been working on Clad, a C++ library that enables Automatic Differentiation using the LLVM compiler infrastructure. It is implemented as a plugin for the Clang compiler.
Clad operates on Clang AST (Abstract Syntax Tree) and is capable of performing C++ Source Code Transformation. When Clad is given the C++ source code of a mathematical function, it can algorithmically generate C++ code for the computing derivatives of that function. Clad has comprehensive coverage of the latest C++ features and a well-rounded fallback and recovery system in place.
Clad’s Key Features:
Support for both, Forward Mode and Reverse Mode Automatic Differentiation.
Support for differentiation of the built-in C input arrays, built-in C/C++ scalar types, functions with an arbitrary number of inputs, and functions that only return a single value.
Support for loops and conditionals.
Support for generation of single derivatives, gradients, Hessians, and Jacobians.
Integration with CUDA for GPU programming.
Integration with Cling and ROOT for high-energy physics data analysis.
Benchmarks show that Clad is numerically faster than the conventional Numerical Differentiation methods, providing Hessians that are 450x (~dim/25 times faster). General benchmarks demonstrate a 3378x improvement in speed with Clad (compared to Numerical Differentiation) based on central differences.
For more information on Clad, please view:
We are part of the
Princeton Department of Physics
and
Princeton Institute for Computational Science and Engineering
(PICSciE).
Contact: David Lange; Vassil Vassilev
This project is supported by National Science Foundation under Grant OAC-1931408 (2020-2023) and OAC-2311471(2023-2026). Any opinions, findings, conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.
© 2019 Princeton University. Site made with Jekyll; Credit to Allan lab for this site template.
