Differentiating electromagnetic showers in a sampling calorimeter
Introduction
I am Max Aehle, a PhD student of Nicolas R. Gauger at the University of Kaiserslautern-Landau, Germany. I have collaborated with Vassil Vassilev and Mihály Novák on applying algorithmic differentiation to HEP simulations.
Motivation
Algorithmic differentiation (AD) is a set of techniques to evaluate derivatives of computer-implemented functions. Recently, AD has begun to be explored for the gradient-based end-to-end optimization of particle detector designs, with potential applications ranging from HEP to medical physics to astrophysics. To that end, the ability to estimate derivatives of the Geant4 simulator for the passage of particles through matter would be a huge step forward.
However, besides the technical challenge of applying AD to over one million lines of code, there is a number of mathematical/statistical challenges: Does the high density of discontinuities, induced for example by ‘if’ and ‘while’ statements in the code, cause problems in the derivative computation? Are we allowed to treat random numbers like constants with respect to AD? How large is the error when the mean pathwise derivative is evaluated as a proxy for the actual derivative of expectancies computed by Monte-Carlo algorithms?
Report
During a four-week stay with the CERN SFT group in November 2023, and another two-week stay in April 2024, we answered these questions for a smaller HEP simulation composed by the G4HepEm and HepEmShow packages. G4HepEm is a toolkit for the simulation of electromagnetic showers, extracting the relevant data and functionalities from Geant4 in a compact and standalone library. HepEmShow uses G4HepEm to simulate electromagnetic showers in a sampling calorimeter with a simple parametric geometry.
After first encouraging results with the novel machine-code-based AD tool Derivgrind, we applied the operator-overloading AD tool CoDiPack to the simulation parts of G4HepEm and HepEmShow. The code for the differentiated G4HepEm and HepEmShow is available on GitHub. It allows us to compute, e.g., the mean pathwise algorithmic derivative of the energy depositions in the layers of the calorimeter, with respect to the initial kinetic energy of the incoming electrons. It turns out that the code is “AD-friendly” once a single process called multiple scattering is disabled. Comparing with the numerical derivatives (difference quotients) of the mean energy depositions, we get only a small deviation of about 5%.
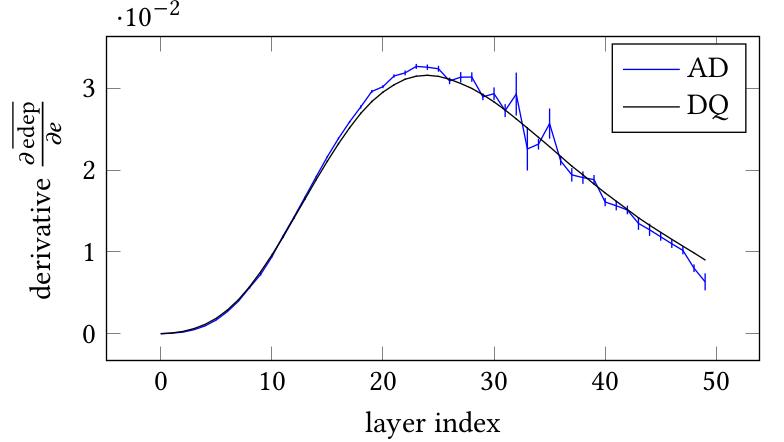
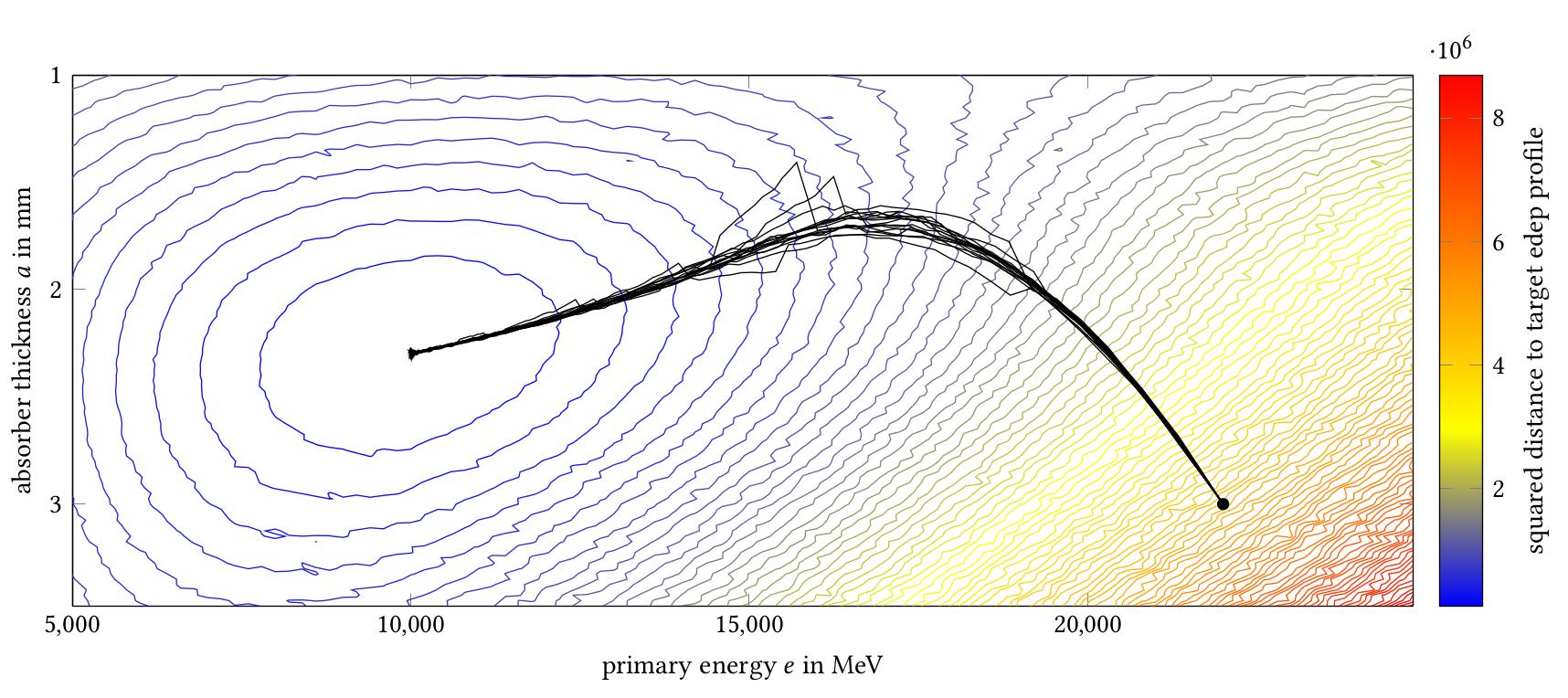
Similar observations can be made for derivatives of the energy deposition with respect to the thickness of the absorber and gap layers in the calorimeter. A small error is not a problem for gradient-based optimization, as we have demonstrated with a simple optimization study shown above, with gradient descent trajectories robustly converging to the minimizer.
Feel free to take a look at our preprint and to get in touch!