How to Execute Gradients Generated by Clad on a CUDA GPU
Tutorial level: Intro
CLAD provides automatic differentiation (AD) for C/C++ and works without code modification (legacy code). Given that the range of AD application problems are defined by their high computational requirements, it means that they can greatly benefit from parallel implementations on graphics processing units (GPUs).
This tutorial showcases how to firstly use CLAD to obtain your function’s gradient and how to schedule the function’s execution on the GPU.
Definition of the custom function
For the purpose of this tutorial, the custom function chosen is the Gauss Function. We include Clad and we defined the function such as:
#include "clad/Differentiator/Differentiator.h"
extern "C" int printf(const char*,...);
#define N 100
__device__ __host__ double gauss(double* x, double* p, double sigma, int dim) {
double t = 0;
for (int i = 0; i < dim; i++)
t += (x[i] - p[i]) * (x[i] - p[i]);
t = -t / (2*sigma*sigma);
return std::pow(2*M_PI, -dim/2.0) * std::pow(sigma, -0.5) * std::exp(t);
}
Definition of Clad gradient
Having our custom function declared, we call Clad gradient and set a device function pointer to be used for the GPU execution:
auto gauss_g = clad::gradient(gauss, "x,p");
//Device function pointer
auto p_gauss = gauss_g.getFunctionPtr();
// using func = void(*)(double* x, double* p, double sigma, int dim,
// clad::array_ref<double> _d_x,clad::array_ref<double> _d_p);
using func = decltype(p_gauss);
Definition of CUDA kernel
The CUDA support for Clad includes extensions that allow one to execute functions on the GPU using many threads in parallel. Thus the kernel for AD execution is to be defined as:
__global__ void compute(func op, double* d_x, double* d_y,
double sigma, int n, double* result_dx,
double* result_dy) {
int i = blockIdx.x*blockDim.x + threadIdx.x;
if (i < n) {
(*op)(&d_x[i],&d_y[i], sigma, /*dim*/1, &result_dx[i], &result_dy[i], nullptr, nullptr);
}
}
Defining variables and stating execution
The next and final step implies the definition of host variables and the copying both of host variables to the device but also of device results back to the host.
The main function carries the role of defining our variables inputs passing them
to the device for the kernel computation and retrieving the results from the
device. This process is done in the following order: we first allocate memory
on the host and define the variables inputs (in our case we have two variables
x and y which are initialised to have random inputs); we then allocate our
device arrays (d_x and d_y) and copy the information from the host to the
device; next, we launch our kernel (“compute”) with the execution configuration
(<<<N/256+1, 256>>>) which translates to the first argument being number of
thread blocks in the grid and the second one (256) being the number of threads
in a thread block and thus having the kernel be executed by these threads in
parallel; the last and final step is to copy the results computed on the device
to the host.
int main() {
// x and y point to the host arrays, allocated with malloc in the typical
// fashion, and the d_x and d_y arrays point to device arrays allocated with
// the cudaMalloc function from the CUDA runtime API
double *x, *d_x;
double *y, *d_y;
double sigma = 50.;
x = (double*)malloc(N*sizeof(double));
y = (double*)malloc(N*sizeof(double));
// The host code will initialize the host arrays
for (int i = 0; i < N; i++) {
x[i] = rand()%100;
y[i] = rand()%100;
}
func h_gauss;
// To initialize the device arrays, we simply copy the data from x and y to
// the corresponding device arrays d_x and d_y using cudaMemcpy
cudaMalloc(&d_x, N*sizeof(double));
cudaMemcpy(d_x, x, N*sizeof(double), cudaMemcpyHostToDevice);
cudaMalloc(&d_y, N*sizeof(double));
cudaMemcpy(d_y, y, N*sizeof(double), cudaMemcpyHostToDevice);
// Similar to the x,y arrays, we employ host and device results array so
// that we can copy the computed values from the device back to the host
double *result_x, *result_y;
result_x = (double*)malloc(N*sizeof(double));
result_y = (double*)malloc(N*sizeof(double));
double *dx_result, *dy_result;
cudaMalloc(&dx_result, N*sizeof(double));
cudaMalloc(&dy_result, N*sizeof(double));
cudaMemcpyFromSymbol(&h_gauss, p_gauss, sizeof(func));
// The computation kernel is launched by the statement:
compute<<<N/256+1, 256>>>(h_gauss, d_x, d_y, sigma, N, dx_result, dy_result);
cudaDeviceSynchronize();
// After computation, the results hosted on the device should be copied to host
cudaMemcpy(result_x, dx_result, N*sizeof(double), cudaMemcpyDeviceToHost);
cudaMemcpy(result_y, dy_result, N*sizeof(double), cudaMemcpyDeviceToHost);
printf("sigma=%f\n", sigma);
for (int i = 0; i < N; i+=10000) {
printf("x[%d]='%f';y[%d]='%f'\n", i, x[i], i, y[i]);
printf("grad_x[%d]='%.10f';grad_y[%d]='%.10f'\n", i, result_x[i], i, result_y[i]);
}
}
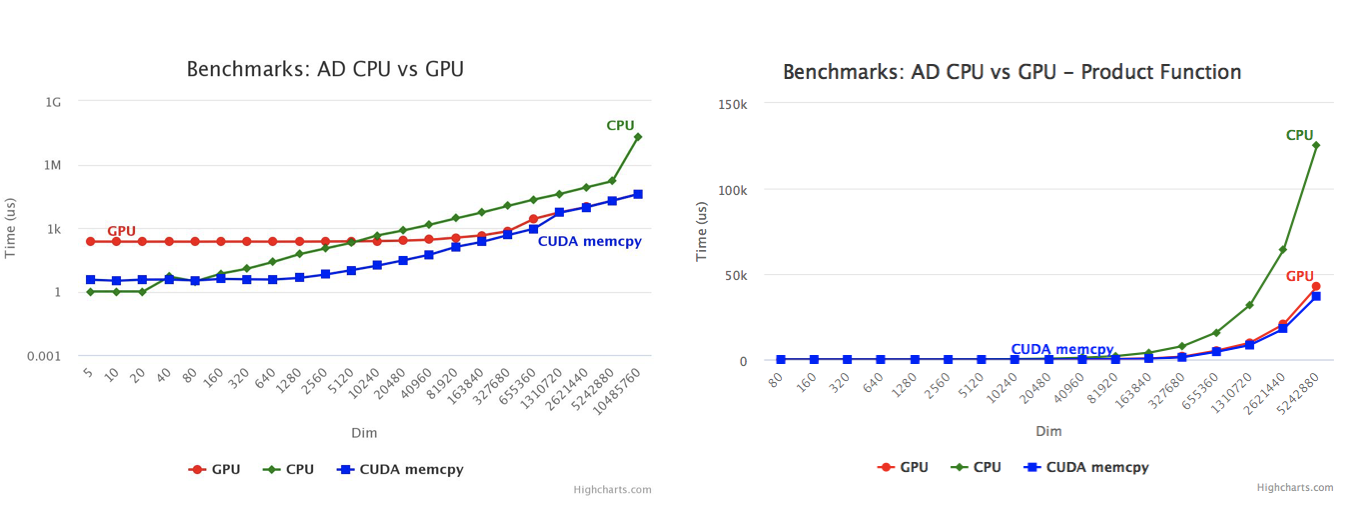
Benchmarking GPU Accelerated Clads
Following the implementation pattern described in this tutorial, will bring forth an increase in performance. The execution time for the GPU implementation decreases with the increase of dimensions, firstly in the case of the above Gauss function and secondly in the case of a product function gradient: